模試の活用
→「一般入試対策=模試対策」
模擬試験(模試)は実際の入試と同レベルの問題が出題され、志望校の合格可能性がわかるテストです。東京都ではVもぎが一般的で、自分の現在地と志望校との差を確認することができます。一般入試の対策を具体的に練ることもできますので、模試は必ず6月から受けておきましょう。
入試は「部分点を取ること」と「ミスを減らすこと」の2点がポイント
模試といっても教科書の内容から出題されるわけですが、定期テストとの違いがあります。模試や入試は(作問者にとって)『平均点が高すぎるとマズい』という事情があります。「難しすぎても」「簡単すぎても」ダメで、できる人からできない人までバランスよく分布している(正規分布という)必要があります。そうでなくては、受験生の相対的な位置を正確に測れないからです。
つまり、入試は(模試も)必ず「難問が混在する」ということです。部分点を積み重ねることが重要で、ケアレスミスは偏差値を下げる要因になってしまいます。
だからこそ入試では、「誰もができる問題を落とさない」ことが大切です。難しい問題(=正答率の低い問題)に時間をかけるより、「部分点を取る」ことの方が重要で、ミスをしなければ偏差値は自ずと上がる傾向があります。
入試(模試)のポイント2点
- 部分点を取ること
- ミスを減らすこと
模試は「正答率の高い問題」を解けることが重要

これがVもぎの各教科(数学)の分析表です。赤い点線の枠内の数字が全受験者の「正答率」です。右端の「正誤」が、自分が『解けた問題〇/間違えた問題×』です。この生徒さんは正答率の高い問題(92%,71%)を落としてしまっています。偏差値は42でした。しかし、正答率60%以上の問題が解けていたら偏差値53まで上がります。「誰もができる問題を落とさない」ことがとても重要です。
偏差値42→(正答率60%以上正解)→ 偏差値53
都立入試『数学』は50%以上が3年生の内容
もちろん1・2年生の内容も出題されますが、3年生の内容がメインになるという点は抑えておいてください。その中でも3年2学期の「円周角の定理」「三平方の定理」「相似な図形」は毎年必ず出題されます。学校の授業では3年生の2学期に扱う内容で、重要事項ですが比較的スピーディーに終わらせてしまうという現状があります。この3点は『3年の夏休みに先取り学習』しておくことをおすすめします。
都立一般入試『数学』の構成
第1問 計算領域 [9問]
①四則演算 ②2文字の整式 ③平方根
④1次方程式 ⑤連立方程式 ⑥2次方程式
⑦確率・データの活用 ⑧作図
⑨図形問題が多い
第2問 思考力領域(論証/証明問題「文字式の利用」)
第3問 関数領域(放物線と直線/直線で囲まれた図形)
第4問 平面図形領域(図形の証明「相似」または「合同」)←ここか⑨で「円周角の定理」
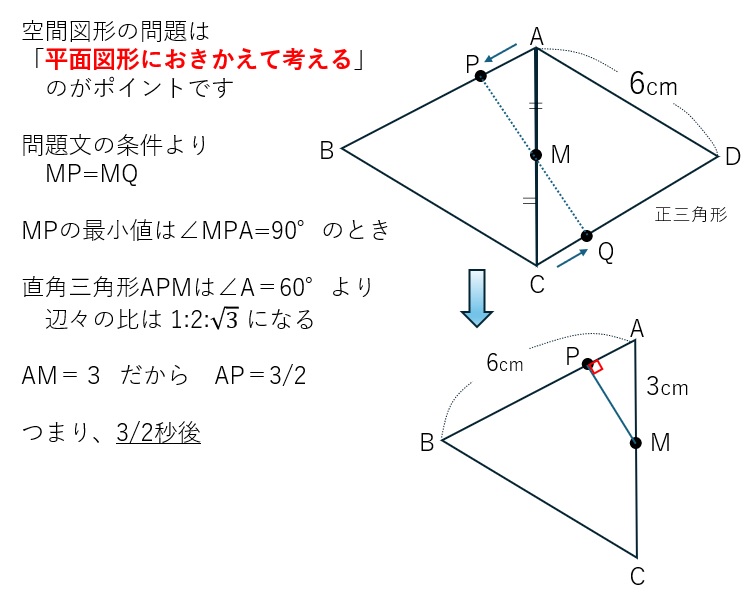
第5問 空間図形領域(動点の考察)←ここで「三平方の定理」
偏差値とは?
偏差値とは「受験生全体の中での自分の位置を数値化したもの」です。どんな試験でも「平均点を取ると偏差値が50になる」ようにできています。この偏差値は点数の「バラつき度合(=標準偏差)」をもとに計算します。「バラつき度合」は平均点に集まっている(または離れている)度合を意味し、中学生対象の模試は1教科で「20点くらい」になるよう作問されています。また、平均点は「40~60点くらい」が一般的です。
(偏差値50)=(平均点)
(偏差値60)=(平均点)+(標準偏差20点くらい)
(偏差値70)=(平均点)+(標準偏差20点くらい)×2

*標準偏差のちがい(平均点はともに50点の5つのデータ)
- [47点,49点、50点,51点,53点]→ 標準偏差:2
- [20点,40点、50点,60点,80点]→ 標準偏差:20
「できなかった」の3段階
模試を受験したあとはそのままにしないで必ず復習をしましょう。その際、重要になるのが正答率を確認して、「わかっていたがミスをした問題(段階1)」「解説を見ればできた問題(段階2)」「解説を見てもできない問題(段階3)」を分解してみることです。模試では「みんなができる問題を確実に正解する」ことが重要で、「みんなができそうにない問題を少しだけ正解する」だけでも偏差値は上げられます。また、時間配分(優先順位)を考える必要もあり「時間がなくて全く手をつけられなかった」問題をゼロにすることも必要です。つまり、「ミスをしない正確性」と「全ての問題をやりきるスピード」が大切であり、これは日頃の練習を積み重ねていくしかありません。
- 段階1 わかっていたがミスをした → すぐにやり直した方がよい問題です
- 段階2 解説(または教科書・参考書)を見ればできた → ここが本来の復習になります
- 段階3 解説(または教科書・参考書)を見てもできない → 今後の課題
都立入試・過去問の分析(数学編)
都立一般入試共通問題(2022年)の数学を見てみましょう。
問題)全問題のうち正答率が30%以下の問題を除き、すべての問題が解けた場合、偏差値はどれくらいになるでしょうか?
≪少し時間を取って考えてみてください≫
答え:偏差値61
みんなができる問題を確実に解ければ「偏差値60を超える」ということです。つまり「ミスをしない正確性」と「時間配分」が大切であり、教科書の内容を網羅的に理解できていることが必須になります。
【都立一般入試共通問題(2023年)数学】
- 正答率が30%を切った問題:20点(第3問3、第4問2②、第5問1、第5問2の4問)
- それ以外の問題の合計:80点
- 偏差値61: 平均点57.6,標準偏差20 → (80-57.6)÷20×10+50=偏差値61.2
参考として、正答率29%(第5問の問1)の問題を見てみましょう。一見すると難しく見えますが、問題文の意味がわかると「それほど難しいわけでもない」ということが理解できると思います。実際に時間をとってやってみてください。
問題PDFはこちら▶東京都教育委員会:都立高校入試問題(数学2023年)
解答)
・関連ページ
「清瀬で高校受験を目指す中学生向け「Vもぎ」模試対策」は▶こちらから
*都立一般入試(学力試験)の概要
都立一般入試は 1020点満点
→ 学力試験:700点(69%) 調査書点:300点(29%) 英語スピーキングテスト:20点(2%)
①学力試験(前期)の仕組み
5教科(国・数・英・社・理)
・実点数500点を → 700点に換算(1.4倍)
・記述問題の部分点が勝負です(=ミスをしないことの重要性)
②調査書点(内申)の仕組み
評価対象は 3年次の9教科評定
計算式 5教科:そのまま + 実技4教科:×2倍
→ 合計65点(25+40)を300点に換算
実技の差は極めて大きい
例)実技4教科 オール3とオール4 → 36点差(学力試験で埋めるのは非常に困難)
※提出物・授業態度・遅刻欠席は即、内申に影響します
③私立高校「併願優遇制度」のしくみ
併願優遇=『事前の内申確認と個別相談で合格がほぼ決まる制度』
私立は 1校しか併願優遇を使えない
中学校の担任と私立高校の合意が必要
調査書点の基準をクリア
個別相談と一般入試を受けることが必須
→ 都立が不合格になれば、この併願校に進学することになるため 慎重な選択が必要
※英検・漢検・数検で加点する学校が多数。
❹自校作成問題(難関10校)について(対象者のみ)
(対象校:日比谷・西・国立・戸山・青山・立川・八王子東・新宿・国分寺・墨田川)
国語・数学・英語のみ自校作成 → 平均点は50〜60点になるよう調整
社会・理科は共通問題
大問の構成・記述量が学校によって強烈に異なる
部分点の積み上げが最大テーマ
スマイルスタディ清瀬では、清瀬市の中学生を対象に、学校ごとの定期テスト対策および志望校を想定した受験対策も行っています。
・清瀬の個別指導塾▶スマイルスタディについて
・内申点(評定)学習サポートは▶こちらから
・当塾の合格実績は▶こちらから

