中学1年生【つまずく分野】:中学数学の3つの壁「①文字式」「②空間図形」「③データの活用」
- 文字式の壁:「xを用いた方程式の文章題(第3章)」&「x, yを用いた比例の文章題(第4章)」
- 空間図形の壁:「(空間図形)円錐の表面積(第6章)」
- データの活用の壁:「データの活用&確率(第7章)」
中学2年生【つまずく分野】:「一次関数の利用」「証明(三角形の合同)」
- 一次関数の応用問題の壁:「傾きが変わる直線の応用」
- 証明の壁:「三角形の合同証明(平行四辺形の成立条件も含む)」
中学3年生【つまずく分野】:「二次関数」「三平方の定理」
- 二次関数:「変化の割合、二次関数の文章問題、放物線と直線」
- 三平方の定理:「入試頻出だが中学では受験直前に扱うことの難しさ」
中学1年生【つまずく分野&勉強法】
3つの壁「①文字式と文章題」「②空間図形」「③データの活用」
② 空間図形の壁
空間図形は、球の体積(4/3πr3)を求めることや高校入試頻出の「作図」などを扱います。その中でも苦手分野の代表格は「立体の展開図」です。円錐(≒アイスのコーン)の表面積(≒周りの面積)は、展開図を書いて求めることになるのですが、これが少し厄介です。この分野は、私たち親世代も苦手意識をもっていた方は多いと思います。基本的に、空間図形の問題は「空間のまま考える」ということはほとんどありません。「空間」→「平面」に置きかえて考えていきます。展開図とは、まさに空間図形を平面に置きかえた模式図になっています。
[空間図形の壁] :円錐の表面積
解き方)空間図形 → 平面に置きかえる(展開図を書く)→ 公式適用 → 計算
ある生徒が難しそうな公式を使って問題を解いていました。その公式が『問題集に載っていた』からだそうです。式の形が複雑なので、その生徒は間違えて公式を使い、答えも間違えてしまいました。このようなことは皆さんもないですか? 問題集に書かれている知識はすべて覚えなければいけないわけではありません。覚えていると便利なものもあるかもしれませんが「理解せずに暗記 → 使える場面があいまい → 間違える」というのでは本末転倒です。時間はかかっても「なぜそうなるか?」を自分で理解する癖をつけてほしいと思います。
例題 「円錐の表面積」が下のような公式で求められる理由を考えてみよう!
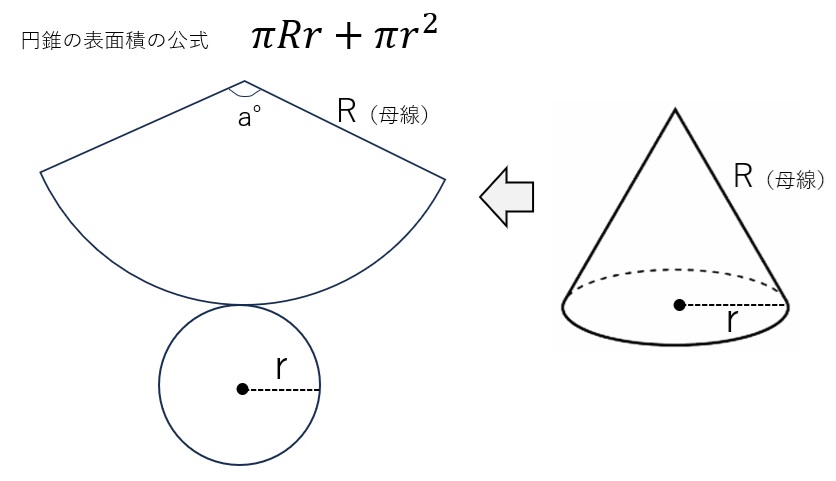
- ある問題集に書いてあった「円錐の表面積」公式です
- 覚えるのが苦手は人は、無理に覚えなくてもよい公式です
- 数学が好きな人で「公式の意味がつかめた」人は覚えると便利かもしれません
- とにかく公式は丸暗記しないこと。暗記するなら理屈を(最低1度は)確認してから問題を解いてください
考え方と解説)

【「空間図形(展開図)の壁」を突破する勉強法】
ポイント:公式成立のプロセスを理解する
- 1つ前の内容(扇形の中心角と弧の長さ)を復習する。
- 『文字式の壁』を突破すること。
- 公式を丸暗記しない。理屈を(最低1度は)確認しながら問題を解く。
数学は“つながりのある学問”なので、前の分野が理解できていないと次の分野にも影響します。だから、「円錐の表面積」を求める前に、「扇形の中心角と弧の長さ」を復習します。解法のプロセスで中心角から弧の長さを求めなくてはならないからです。
また、『1.文字式の壁』を突破した子は、「公式にも理屈がある」ということがわかります。だから「なんで、(扇形の弧の長さ)=(底面積の円周) が成り立つか?」に意識が向くようになるのです。そうすると、立体的なイメージを平面に置き換える思考が働くのでしょう。一旦、納得がいけば忘れることはありません。解法のプロセスをその都度意識して解くようになるからです。

「公式の背景を理解して解くこと」と「理解しないで解くこと」の差は大きいと思います。「なんだかよくわからない」ことをやらされるのは誰でも苦痛ですよね。これでは内発的な動機付けは働きません。つまり、自分で問題を解くことから避けるようになります。演習量が足りていないのですから定着しません。悪循環です。ただし上の3点を押さえても、理解できない生徒は一定数出てきます。そのときは「実際に紙から円錐を作ってみる」ということが重要です。解けないことに苛立って、精神的な余裕がなくなっている生徒は、この作業をしたがりません。その場合も、「とにかく焦らない。焦らせない。」ことが重要です。
【都立一般入試共通問題(2022年)数学の第5問】
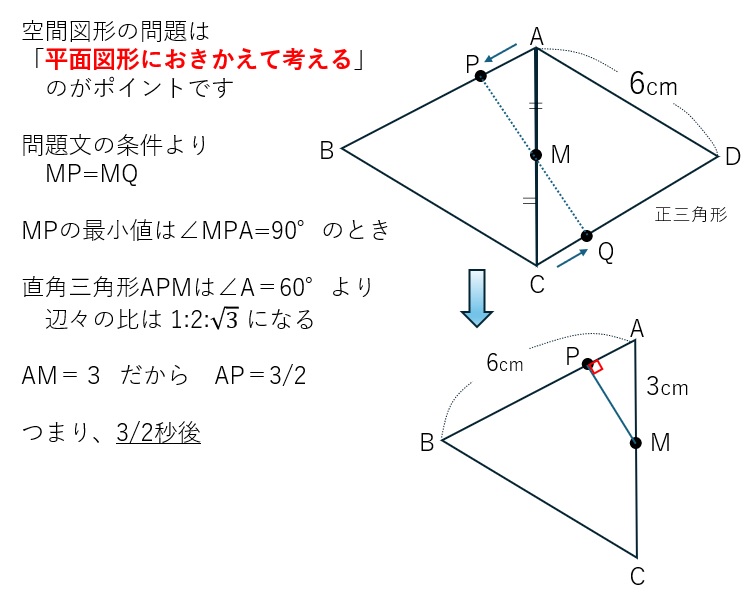
参考として、(3年生を対象に)都立一般入試の問題「空間図形(正答率29%)」を見てみましょう。一見すると難しく見えますが、問題文の意味がわかると「それほど難しいわけでもない」ということが理解できると思います。実際に時間をとってやってみてください。

解説) 空間図形 → 平面に置きかえる(展開図を書く)→ 公式適用 → 計算