高校入試と大学入試の難易度の差
皆さんは高校入試と大学入試の難易度の差はどれくらいだと思いますか?
受験を終えた3年生に聞くと、だいたいの生徒が「10倍くらいかな」と答えてくれます。それ以上と答える人もいましたが、平均的には10倍くらいという感じです。この数値は難易度を人口比と大学の首都圏集中度から概算した結果とだいたい一致します。
例.「首都圏の大学を受ける場合、大学入試と高校入試の難易差にはどれくらいの差が出るか?」
- 高校と大学の進学割合:高校進学率98%,大学進学率55%
→ 1.8倍(0.98÷0.55=1.78…)
- 大学の首都圏集中度:40%
→ 全国の大学入学者の41%が東京,神奈川,埼玉,千葉の大学に集中している。
→ 東京都中学3年生(15歳)の人口比:8%
→ 5.1倍(0.41÷0.08=5.125)
つまり、難易差 5.1×1.8=9.2倍
高校入試 → 大学入試:9.2倍

高校入試と大学入試(首都圏の大学)では、受験者数がおよそ9倍~10倍違うと考えてよさそうです。逆に考えると、地方大学は入りやすくなっているという見方もできます。
模擬試験について
高校入試との比較で、大学入試が約10倍違うという話をしました。では、その大学入試は何を基準に学習計画を立てればよいでしょうか?
その軸となるのが模擬試験の結果です。もうすでに模試の大切さは理解していると思いますが、それを実践できている人はどれくらいいるでしょうか? 数学であれば、チャートやサクシードなど多くの問題集が市販されています。その中で最も新傾向を反映させた“問題集”は模試(駿台や河合模試も含め)の過去問です。模試は来年度入試の傾向を調査し、時間をかけて作問されます。予備校の講師が3ケ月以上の時間と労力をかけてつくる訳ですから、市販の問題集よりもタイムリーな問題が多く掲載されているのです。校内(または校外)受験した模試は、解説とともにすべてファイリングして大切に保管しておいてください。
問題.「5科解説付きの模試セットはどれくらいの価値があると思いますか?」
2020年のことですが、進研模試(5科解説付き)がオークションサイトで15,000円で出品されているのを見ました。それだけの価値があるということです。校内受験した模試は、解説とともにすべてファイリングして大切に保管してください。

偏差値の意味を知ろう!
偏差値とは…

(標準偏差:点数の散らばり具合を数値化したもの)
偏差値とは「受験生全体の中での自分の位置を数値化したもの」です。どんな試験でも「平均点を取ると偏差値が50になる」ようにできています。また、偏差値は点数の「ばらつき度合(=標準偏差)」をもとに計算します。例えば、A君50点、B君51点、C君49点なら「標準偏差」は1点です。A君50点、B君60点、C君40点なら「標準偏差」は10点です。つまり、標準偏差は平均点に集まっている(または離れている)度合を意味します。中学生対象の模試は1教科で、標準偏差は「15~20点」、平均点は「60点くらい」になるように作問されています。一方、高校生を対象とした模試は(100点満点なら)標準偏差は「15~25点」、平均点は「40~50点くらい」になるはずです。
- (偏差値50)=(平均点)
- (偏差値60)=(平均点)+(標準偏差)
- (偏差値70)=(平均点)+(標準偏差)×2
進研模試の結果をもとに「偏差値の計算方法」を確認してみましょう。大学入試の場合は100点満点ではなく200点満点の試験が多いので、その場合の算出法を考えてみます。
例えば、2年生1月の記述模試:英語で偏差値60になるには何点取ればよいでしょうか?
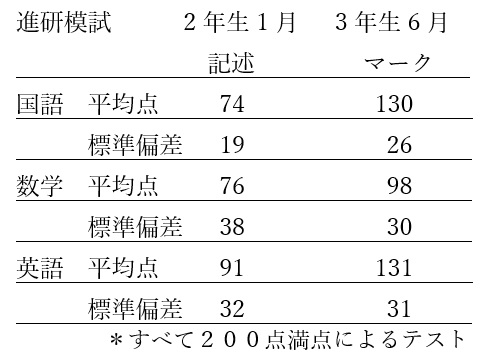
(X-91)÷32×10+50=60 を解いて
(X-91)÷32×10=10 → X-91=32 よって、X=123
つまり、123点(200点満点)取れば偏差値が60になるということです。計算方法がわかればそこまで難しいわけではないですよね。
偏差値60を目指すには…
まず、教科書の内容は確実に身につけ、誰もができる問題を落とさないことが重要です。ケアレスミスがあれば平均点をとることも難しくなります。そして、配点を調べたうえで+標準偏差(30点)分を取ればよいのですから、「できる可能性があったけど間違えた問題」と「今やってもできなかった問題」を分けて復習することが必要になります。
「できなかった」の3段階
- 段階1 わかっていたがミスをした。
- 段階2 教科書・参考書を見ればできた。
- 段階3 教科書・参考書を見てもできない。
段階1はケアレスミスです。段階2は忘れてしまった部分なので再度練習し、確認しておく必要があります。段階3は「今後の課題」であり、この部分をできるようにすることが本来の復習です。わからなければ聞く必要があるかもしれません。主観的にならないよう、常に客観的に対策を立ててください。

教科書の重要性について
共通テストの対策として最も重視すべき参考書は何でしょうか?
いろんな問題集が出てくると思いますが、最も重要なものは教科書です。その理由を、共通テスト数学を参考にしながら確認していきます。共通テストの数学で強調されているポイントは以下の3点です。
- 「言葉の視覚的イメージ」
- 「公式そのものの理解(または導出過程)」
- 「解法の段階的な深い洞察」
1の例は「弧度法の1ラジアンとは何か?(2018センター数ⅡB)」や「四分位数とは?(2020センター数ⅠA)」など、定義そのものを問う問題です。弧度法はその典型で『60°を弧度法に直せ』という問題なら誰でも解けます。しかし、弧度法そのものの定義を聞かれると困ってしまう人は多いのではないでしょうか? そのような定義が問われた場合、戻るべきはやはり教科書です。教科書の内容をしっかりと理解し「自分の言葉で説明できる」段階になれば、共通テストは解けるようにできています。これは数学だけでなく世界史や英語も同様です。

2「公式そのものの理解(または導出過程)」は、例えば『三角関数の合成公式の過程』を問う問題です。三角関数の合成は「sin(θ+α)」のようにsinでしかできないようだと、共通テストには対応できません。公式の成立ちを理解していれば「cosでも合成できる」ということがわかるはずです。これも共通テスト2021年で出題されました。教科書の内容を「自分の言葉で説明できる」ようになるまで習熟しておく必要があります。
3「解法の段階的な深い洞察」の例としては、数Ⅱの教科書の一般的な問題を『共通テスト』風にアレンジしてみました。教科書の問題と言っても侮れません。





