【都立高校一般入試(前期)について】
- 都立一般入試は調査書点が加味される
- 英語スピーキングテストの点数も加味される
- 学力試験は国語・数学・英語・社会・理科の5教科が出題される(私立は3教科が多い)
- 自校作成校は、日比谷、国立、西、戸山、青山、立川、八王子東、新宿、国分寺、墨田川で「国語、数学、英語」が自校作成問題となり、社会、理科は共通問題になる(国際高校は英語のみ自校作成)
- 都立受験者も私立高校の併願優遇制度を理解しておく
都立一般入試「学力試験」「調査書点」「スピーキングテスト」の対策
受験勉強は事実(=データ)にもとづいて戦略を立てることが大切です。計算式がたくさん登場しますが意味がわかるとそこまで難しくないはずですので、自分の手を動かして考えてみてください。これも一つの受験勉強です。自分で手を動かしながら具体的に考えていくと「何をやるべきか」が明確になります。
- 都立一般入試の得点比率
①学力試験700点 (69%)+②調査書点300点 (29%)+③スピーキングテスト20点 (2%)=1020点満点 (100%)
①学力試験について
学力試験(学力考査点)は5教科で100点ずつの合計500点満点です。その合計点を500で割って700倍することで学力考査点を出します。
学力考査点は実際の点数を1.4倍(1.4=700点/500点)して計算するので、「わからなかったとしてもあきらめない」で部分点を少しでも多く取ることが重要です。特に、記述問題では時間配分にもよりますが、わからなくても「わかることを整理しておく」ことが必要です。例えば、当日の試験(5教科)で3点ずつ増えると15点(3点×5教科)増えることになります。それが1.4倍されると21点分(15点×1.4倍=21点)が増えるわけです。これだけで、スピーキングテストの20点分を超えることになります。
例1)国語:66点、数学55点、英語72点、社会71点、理科60点 の場合(合計324点)
→ 324点/500点×700点=453点(1020点) [学力考査点]
「各教科で3点ずつ増えた場合」
例2)国語:69点、数学58点、英語75点、社会74点、理科63点 の場合(合計339点)
→ 339点/500点×700点=474点(1020点) [学力考査点] 差:21点
②調査書点について
調査書点は、中学3年次のみが対象で『5教科はそのまま、実技4教科は2倍して計算します』。ただし、3年生の成績は、たいていの学校で1,2年次の成績を考慮してつけているようです。3年次だけで大幅に成績が上がることは少ないので1,2年から成績を上げておく必要があります。もうすでに1学期は始まっていますが、後悔しても生産性はありません。「提出物を出す」「授業に参加する(寝ない)」「実技教科のテストも頑張る」など、今日からできることを今すぐ実践していきましょう。
調査書点は、3年生の9教科評定を使用し、その合計は65点(5×5科+5×4科×2倍=65)です。その9科の評定(合計)を65で割って300倍します。5教科(国数英社理)はそのままで、実技4教科(保健体育、技術家庭、音楽、美術)は2倍して計算します。
例えば、実技4教科が「オール3」と「オール4」では差が4点(4教科で)しかありませんが、実際の点数は2倍(実技4教科)と4.6倍(4.62=300/65)で9.2倍の差(4点→[9.2倍]→36.8点)が出るわけです。当日の学力試験で37点(4点×2倍×4.6倍≒37点)の差を埋めることは非常に困難です。
- 実技4科オール3の場合
3×4科×2倍=24点 → 24点/65点×300点=110点
- 実技4科オール4の場合
4×4科×2倍=32点 → 32点/65点×300点=147点 差:37点
内申点は、実技4科に力を入れた場合とそうでない場合で大きな差が出てしまいのが都立高校入試の特徴です。当日の学力試験の5教科トータルで60点くらい差が出てしまいます。学力試験1教科あたりで換算すると12点です。それだけ大きな差が出てしまうということは意識しておいてください。
- 「実技4科を重視していない成績」
国語3、数学5、英語4、社会4、理科3、保健体育3、技術家庭3、音楽2、美術2
5教科:19点(25点中)、実技4教科:10点(20点中) → 19点+(10点×2倍)=39点
合計39点/65点×300点=180点 [調査書点]
- 「実技4科を頑張った場合の成績」
国語3、数学5、英語4、社会4、理科3、保健体育4、技術家庭4、音楽4、美術5
5教科:19点(25点中)、実技4教科:17点(20点中) → 19点+(17点×2倍)=53点
合計53点/65点×300点=244点 [調査書点] 差:64点
③英語スピーキングテスト得点(ESAT-J)について
試験ではタブレット端末、ヘッドフォン、イヤホンマイクを使用し「英文の読み上げ」「質問への応答」「自分の意見を述べる」等の問題が出題されます。3年の11月下旬頃に実施され6段階で評価されます(2023年実施結果の割合)。
→ A:20点(17%)、B:16点(26%)、C:12点(32%)、D:8点(17%)、E:4点(8%)、F:0点(1%)

事実を知り「できること」を実践することの重要性
例1)対策をしない場合
- 国語:66点、数学55点、英語72点、社会71点、理科60点(①学力検査点453点)
- 国語3、数学5、英語4、社会4、理科3、保健体育3、技術家庭3、音楽2、美術2(②調査書点180点)
- スピーキングテスト:B(③スピーキング16点)
→ ①学力試験453点+②調査書点180点+③スピーキングテスト16点=649点(得点率:64%)
例2)対策をした場合
- 国語:69点、数学58点、英語75点、社会74点、理科63点(①学力検査点474点)
- 国語3、数学5、英語4、社会4、理科3、保健体育4、技術家庭4、音楽4、美術5(②調査書点244点)
- スピーキングテスト:B(③スピーキング16点)
→ ①学力試験474点+②調査書点244点+③スピーキングテスト16点=734点(得点率:72%)
本番の試験で3点増やすことならできそうですよね。また、実技4科の成績を上がることなら決して難しいわけではありません。このわずかな違いが、本番の試験で85点の差を生むことになります。85点もの差がつくなら、本当に逆転もありえるかもしれませんね。
【都立一般入試(前期)のポイント】
- 学力試験は5教科で実施され、「部分点を少しでも多く取る」ことが重要になる
- 特に記述問題はわからなくても「わかることを整理する」習慣をつけておく
- 学校の定期テストの延長に入試問題があることを理解し、定期テストをおろそかにしない
- 調査書点は実技4教科(保健体育、技術家庭、音楽、美術)のみ2倍して計算する
- 調査書点は中学3年次のみの成績が対象となり、総合点(1020点)の約30%の割合になる。ただし、3年生の成績は、たいていの学校で1,2年次の成績を考慮してつけている。
- 「提出物を出す」「授業に参加する(寝ない)」「実技教科のテストも頑張る」など当たり前のことを継続する
- 英語スピーキングテスト得点の割合はおよそ2%(20点/1020点)である

模試の活用法
模擬試験(模試)は実際の入試と同レベルの問題が出題され、偏差値や志望校の合格可能性がわかるテストです。自分の現時点での学力と志望校との差が理解できるので目標が立てやすくなります。本番の予行演習として受ける人が多いのも特徴です。模試と言っても、教科書の内容を確実に身につけ誰もができる問題を落とさないことが重要です。ケアレスミスがあれば、平均点をとることも難しくなってしまいます。難しい問題を勉強するよりも「ミスを減らす」ことの方が重要です。なぜなら、模試は『誰もができる問題ばかりではない』からです。
・偏差値とは?
偏差値とは「受験生全体の中での自分の位置を数値化したもの」です。どんな試験でも「平均点を取ると偏差値が50になる」ようにできています。また、偏差値は点数の「ばらつき度合(=標準偏差)」をもとに計算します。例えば、A君50点、B君51点、C君49点なら「ばらつき度合」は1点です。A君50点、B君60点、C君40点なら「ばらつき度合」は10点です。つまり、「ばらつき度合(=標準偏差)」は平均点に集まっている(または離れている)度合を意味します。中学生対象の模試は1教科で、ばらつき度合(標準偏差)は「15~20点」、平均点は「60点くらい」になるように作問されています。
- (偏差値50)=(平均点)
- (偏差値60)=(平均点)+(20点くらい:標準偏差)
- (偏差値70)=(平均点)+(20点くらい:標準偏差)×2
・「できなかった」の3段階
模試を受験したあとはそのままにしないで必ず復習をしましょう。その際、重要になるのが配点を調べたうえで、「わかっていたがミスをした問題(段階1)」「解説を見ればできた問題(段階2)」「解説を見てもできない問題(段階3)」を分解してみることです。模試では「みんなができる問題を確実に正解する」ことが重要で、「みんなができそうにない問題を少しだけ正解する」だけでも偏差値は上げられます。また、時間配分(優先順位)を考える必要もあり「時間がなくて全く手をつけられなかった」問題をゼロにすることも必要です。つまり、「ミスをしない正確性」と「全ての問題をやりきるスピード」が大切であり、これは日頃の練習を積み重ねていくしかありません。
- 段階1 わかっていたがミスをした → 「すぐにやり直す問題」
- 段階2 解説(または教科書・参考書)を見ればできた → 「ここが本来の復習です」
- 段階3 解説(または教科書・参考書)を見てもできない → 「今後の課題」
・「過去問」の分析(数学編)
都立一般入試共通問題(2022年)の数学を見てみましょう。全問題のうち、難しい問題(正答率が30%以下)をのぞいて、すべての問題が解けたと仮定します。これで偏差値はどれくらいになると思いますか?
これだけで偏差値は61になります。みんなができる問題を確実に解ければ「偏差値60を超える」ということです。つまり「ミスをしない正確性」と「スピード」が大切であり、教科書の内容をしっかりと理解できていることが大前提になります。
【都立一般入試共通問題(2022年)数学】
- 正答率が30%を切った問題:「第3問の問3、第4問の問2②、第5問の問1と問2」の計4問
- それ以外の問題を合計した点数:80点
- 偏差値61 ( 平均点57.6,標準偏差20として計算すると → (80-57.6)÷20×10+50=偏差値61.2 )
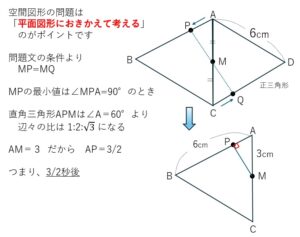
参考として、正答率29%(第5問の問1)の問題を見てみましょう。一見すると難しく見えますが、問題文の意味がわかると「それほど難しいわけでもない」ということが理解できると思います。実際に時間をとってやってみてください。

解説)