「わかる」と「できる」は別物です
「わかる」だけで問題は解けるようにはならないんです。自分一人で「(問題が)できる」ようになって初めて成績は上がっていきます。今はわかりやすい教材や動画があふれているので、「わかった」状態になることはそう難しくありません。しかし、「わかった」と思って実際に問題を解いてみると、答えが合わないということは多いのではないでしょうか。「わかった」知識を手がかりに、自分で「解ける(=できる)」段階にもっていくことが大切です。まずは「わかること」と「できること」がどのように違うのか、具体的な例を通して確認していきましょう。
わかるとは?
内容や説明に納得できた状態です。
同じ説明を聞いても、納得できる人とできない人は出てきます。10人いたら10通りの「わかった」があり、他の人の「わかった」度合をあなたが知ることはできません。だから「わかった」という状態が『どのような状態なのか?』を知ることは意外と難しいのです。では、その「わかった」度合の差はどこから生まれるのでしょうか?
「わかる」ためには、前提となる知識が必要です!
生徒は皆「私は頭が悪いから、わからない…」と言ったりします。本当にそうでしょうか? 私は、頭の良し悪しではなく、前提となる「知識があるかどうか?」が「わかる度合」の差を生み出していると考えています。実際に問題を通してその違いを考えてみましょう。まず、下の問題&解説を読んでください。前提となる知識があるかどうかで、「わかる」度合が変化するということがわかってもらえるはずです。
≪❶前提となる知識が“ない”場合≫
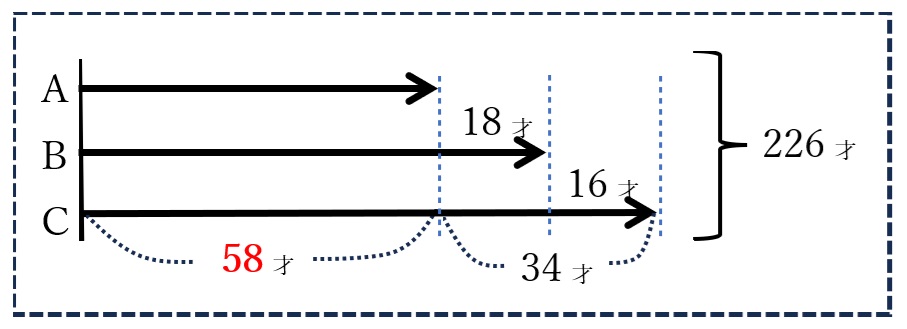
[問題1] 太郎君にはA、B、Cの3人の祖父母がいます。3人の年齢の合計は226才で、BはAより18才年上、CはBより16才年上です。このとき、A,B,Cの年齢を求めなさい。
[解説]
CはAより18+16=34(才)上なので
Aにそろえると、226-(18+34)=174(才)
これがAの3人分にあたるので
Aは 174÷3=58(才)
よって、A:58才、B:76才、C:92才
「なんとなくわかったような、わからないような…」という感じの人は多いのではないでしょうか。私もこのような経験を何度も繰り返してきました。言葉にはできないけど「なんとなく納得できない」状態ですよね…。
次は、前提となる知識(例題)を確認した後に、同じ問題&解説を見ていきます。
≪❷前提となる知識が“ある”場合≫
[例題]…前提となる知識
太郎君にはA、Bの2人の祖父母がいます。2人の年齢の合計は150才で、BはAより18才年上です。このとき、A,Bの年齢を求めなさい。
[解説]
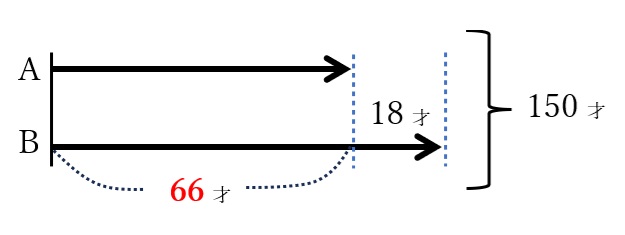
BはAより18(才)上なので
Aにそろえると、150-18=132(才)
これがAの2人分(=132)にあたるので
Aは 132÷2=66 (才)
よって、A:66才、B:84才
↓
[問題1] 太郎君にはA、B、Cの3人の祖父母がいます。3人の年齢の合計は226才で、BはAより18才年上、CはBより16才年上です。このとき、A,B,Cの年齢を求めなさい。
[解説]
CはAより18+16=34(才)上なので
Aにそろえると、226-(18+34)=174(才)
これがAの3人分にあたるので
Aは 174÷3=58(才)
よって、A:58才、B:76才、C:92才
問題文の条件を図に表すことができれば、[解説]を理解する手がかりになります。その部分を、前提となる知識(例題)で補うことができるかどうかが「わかる」ための分岐点です。
問題1の解説)
CはAより18+16=34(才)上なので、
Aにそろえると、226-(18+34)=174(才)
これがAの3人分にあたるので
Aは 174÷3=58(才)
よって、A:58才、B:76才、C:92才
問題1の別解) 連立方程式を使う解法

説明は階段上になっている
説明には階段があります。「AがわかったらB」→「BがわかったらC」→「CがわかったらD」→…という感じです。先ほどの、❶「前提となる知識がない場合」と❷「前提となる知識がある場合」では下のようなイメージになります。

前提の知識がない状態で説明されると「なんか納得できない…」ということは多いと思います。知識がある人は、その知識を使って説明の飛躍している部分を自分で埋めることができます。知識がない人にとっては、「どこが」「どのように」飛躍しているかがわからないので『わからないことがわからない』状態になってしまいます。この『わからないことがわからない』状態は、誰しも一度は経験しているはずです。左図のように、いきなり高い階段を一気に上ることはできません。順番に理解していく必要がありますし、重要なのは「自分に前提となる知識があるか?」どうかを確認することです。知識があれば階段を順番に上がることはできます。しかし、知識がなければ階段は上がれません。勉強はどんな科目でも「知識が必要になる」からです。そして、その階段が見えない構造になっている科目の代表格が、数学なのです。

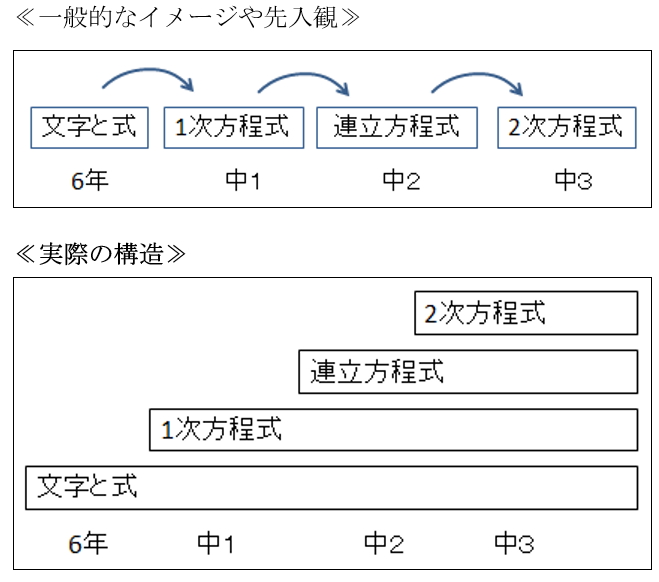
勉強も階段状(=積み重ね学習)になっている
数学だけでなく、すべての教科が『積み重ね学習』であり、基礎に応用が重なり階段のような構造になっています。その構造がはっきりしている教科が数学です。≪一般的なイメージ≫のように各単元が別々に連なっているわけではありません。≪実際の構造≫のように階段状になっています。例えば、中学3年の「2次方程式」がわからない場合、2次方程式が理解できないのではなく、2次方程式以外でつまずいている可能性があります。断定はできませんが、中3の内容でつまずいたら、場合によっては小6の内容に戻らなければいけないのです。本人に自覚できないところが難しいのですが…。
「わかった」ことを整理することの重要性
勉強とは、この「わかった」ことを自分で整理してみる作業も含まれます。勉強の大半は、わかったことを前提にして、問題を自分で「できる」ようにすることです。しかし、それだけでは階段を上がれないことがあります。説明はわかったけど、問題を解いてみると正答にたどり着けないという場合です。
そんなときは下の3つのどれかが原因です。少し時間をとって振り返ってみましょう。
- (前提となる)知識が身についていない
- 問題の難易度が高すぎる(階段の段差が高すぎる)
- 読解力が足りない(問題文が正確に読めていない)→ 「今回はこの部分には触れません…」

数学や理科であれば「わかった」ことを図に表すことが重要になります。目に見える形(=視覚化)に変えていくと、問題文のポイント(意味)が自分なりに納得できるようになるからです。国語や英語なら、「わかった」ことを他の人に説明してみるというのも有効です。逆にいうと、「わかった」ことを『図に表せない』または『説明できない』ということなら、それは「わかっていない」場合がほとんどです。

まとめ
🔻「わかる」ために必要なこと
- (その問題を解くための)前提となる知識が身についている(=暗記できている)
- 数学や理科なら「わかった」ことを図に表すことができる
- 国語、英語、社会なら、「わかった」ことを他の人に説明することができる
- 選択肢問題なら、正しくない選択肢の「正しくない理由」を指摘することができる
🔻問題を解いたが正答にたどり着けない理由
- (前提となる)知識が身についていない(=暗記できていない)
- 問題の難易度が高すぎる
- 読解力が足りない(問題文が正確に読めていない)
→ 「わかる」を「できる」に変える勉強法(後編)へ続く

